算法—-局部搜索算法

要求：

生成一个无向连通图，有100个点，1000条边，边上的权重是1到20之间的随机整数。

用局部搜索算法实现，再用Kruskal或prim算法进行验证。

---

局部搜索算法的基本思路：

1. 设法得到一棵生成树T
2. 检查不在T上的边，如果加上一条边，生成一个环，并删除一条环上的最大权重的边
3. 重复2，直到所有边都不能优化为止。

对于以上要求和思路，我们可以一步一步地实现：

1. 生成无向连通图

   这里，我采用链表的形式存储。

   struct Node {//链表节点
   	Node(int x, int y, int z, int q);
   	int vseq;//x
   	int vseq2;//为了记录边增加的属性，q
   	int eseq;//z
   	int weight;//权重1-20,y
   	Node *next;
   };
   Node::Node(int x, int y, int z, int q) {
   	vseq = x;
   	vseq2 = q;
   	weight = y;
   	eseq = z;
   	next = NULL;
   }
   class List {
   public:
   	List();
   	bool Find(int x);//找点
   	bool Finde(int z);//找边
   	int finde(int x, int y);//根据点得到边序号和权重
   	void PushBack(int x, int y, int z, int q);
   	void Sort();
   	void PrintList();
   	void MovNode(Node *p);//delete the node which data=x
   	void PopBack();
   	void PopFront();
   	int count;
   	Node* head;
   	Node* tail;
   };
   List::List() {
   	head = NULL;
   	tail = NULL;
   	count = 0;
   }
   bool List::Find(int x) {
   	if (head == NULL) {
   		//cout << "empty" << endl;
   		return false;
   	}
   	else {
   		Node* p = head;
   		while (p != NULL) {
   			if (p->vseq == x) return true;
   			p = p->next;
   		}
   		return false;
   	}
   
   }
   int List::finde(int x, int y) {
   	if (head == NULL) {
   		//cout << "empty" << endl;
   		//return;
   	}
   	else {
   		Node* p = head;
   		while (p != NULL) {
   			if (p->vseq == x  ) 
   				return p->eseq;
   			p = p->next;
   		}
   		//return;|| (p->vseq2 == x && p->vseq == y)&& p->vseq2 == y
   	}
   
   }
   bool List::Finde(int z) {
   	if (head == NULL) {
   		//cout << "empty" << endl;
   		return false;
   	}
   	else {
   		Node* p = head;
   		while (p != NULL) {
   			if (p->eseq == z) return true;
   			p = p->next;
   		}
   		return false;
   	}
   
   }
   void List::PushBack(int x, int y, int z, int q) {
   	if (head == NULL) {
   		head = new Node(x, y, z, q);
   		tail = head;
   	}
   	else {
   		tail->next = new Node(x, y, z, q);
   		tail = tail->next;
   	}
   	count++;
   }
   void List::Sort() {
   	int temp;
   	if (head == NULL)
   		return;
   	for (int i = 0; i < count - 1; i++) {
   		Node* left = head;
   		Node* right = head->next;
   		if (left->vseq > right->vseq) {
   			temp = left->vseq;
   			left->vseq = right->vseq;
   			right->vseq = temp;
   		}
   		right = right->next;
   		left = left->next;
   	}
   }
   void List::PrintList() {
   	if (head == NULL) {
   		cout << "empty" << endl;
   		return;
   	}
   	else {
   		Node* tmp = head;
   		while (tmp != NULL) {
   			cout << "-->" << tmp->vseq;
   			cout << "," << tmp->weight;
   			tmp = tmp->next;
   			
   		}
   		cout << endl;
   	}
   }
   void List::MovNode(Node *p) {
   	if (p == tail) {
   		PopBack();
   	}
   	else if (p == head) {
   		PopFront();
   	}
   	else {
   		Node *pp = head;
   		while (pp->next != p) {
   			pp = pp->next;
   		}
   		pp->next = p->next;
   		delete p;
   	}
   	count--;
   }
   
   void List::PopBack() {
   	if (head == NULL)
   	{
   		//cout << "empty" << endl;
   		//return;
   	}
   	else if (head == tail)
   	{
   		delete head;
   		head = NULL;
   		tail = NULL;
   	}
   	else
   	{
   		Node* cur = head;
   		while (cur->next != tail)
   		{
   			cur = cur->next;
   		}
   		delete tail;
   		tail = cur;
   		tail->next = NULL;
   	}
   }
   void List::PopFront() {
   	if (head == NULL)
   	{
   		//cout << "empty" << endl;
   		return;
   	}
   	Node* tmp = head;
   	head = head->next;
   	tail->next = NULL;
   	delete tmp;
   }

   需要的存储结构

   struct Edge {//链表节点
   	//Node(int x, int y, int z, int q);
   	int vseq;//x
   	int vseq2;//为了记录边增加的属性，q
   	int eseq;//z
   	int weight;//权重1-20,y
   	//Node *next;
   };
   struct Vertex {//顶点   
   			   //Vertex(int x);
   	int seq;//0-99
   	int color;//whilte-0,gray-1,black-2
   	int d;//discovet time
   	int f;//finish time
   	int parent;//π
   			   //Vertex *next;
   	bool has = false;//是否有邻接点进栈
   	//int set = V;
   };
   List e[V];//100个点，每个点一个链表
   List e2[V];//找环的链表
   Edge e3[E];//存储边的信息，找权重
   Vertex v[V];//dfs
   Vertex v2[V];//circle
   int t = 0;//time
   stack<Vertex> st;//DFS
   stack<Vertex> st2;//找环的DFS
   Vertex tmp;//top
   Node *p = NULL;//head
   int pp = 0;//p.seq
   Node *ppp = NULL;
   int countt = 0;
   List tree;//生成树
   List cir;//求环
   stack<Edge> ntree;//不在树上
   Node *l;

   随机生成无向图

   int randomnum()//返回一个0-99之间的随机数
   {
   	int a;
   	//srand(0);//设置随机数种子，使每次运行获取的随机数不同
   	a = rand() % V;
   	return a;
   }
   int randomnum2()//返回一个0-19之间的随机数
   {
   	int b;
   	//srand(0);//设置随机数种子，使每次运行获取的随机数不同
   	b = rand() % 20;
   	b++;
   	return b;
   }
   //生成无向连通图
   void creDGra() {
   	//n个点，至少n-1条边
   	int a, b, c;
   	//Node v[V];//100个点
   	for (int i = 0; i < E; i++) {
   		a = randomnum();
   		b = randomnum();
   		c = randomnum2();//weight
   		if (!e[a].Find(b) && a!=b) {
   			e[a].PushBack(b,c,i,a);
   			e[b].PushBack(a,c,i,b);
   			e3[i].eseq = i;
   			e3[i].vseq = a;
   			e3[i].vseq2 = b;
   			e3[i].weight = c;
   		}
   		else {
   			i--;
   		}
   	}
   }

2. 找出一棵生成树T

   这个利用DFS就可以实现，这里写的是利用栈实现的非递归DFS。

   //生成树
   void DFS() {//not ..
   			//cout << "start with " << s << endl;
   			//initialize
   	for (int i = 0; i < V; i++) {
   		v[i].seq = i;
   		v[i].color = WHITE;
   		v[i].d = -1;
   		v[i].f = -1;
   		v[i].parent = V;
   	}
   	//push the first
   	for (int s = 0; s < V; s++) {
   		if (v[s].color == WHITE) {
   			//cout << v[s].seq << endl;
   			v[s].color = GRAY;
   			v[s].d = t;
   			t++;
   			st.push(v[s]);
   			while (!st.empty()) {
   				tmp = st.top();
   				//cout << tmp.seq << " color:" << tmp.color << endl;
   				if (v[tmp.seq].color == BLACK) {
   					st.pop();
   				}
   				//cout << "top: " << tmp.seq << endl;
   				//adjacent
   				p = e[tmp.seq].head;
   				for (int i = 0; i < e[tmp.seq].count; i++) {
   					pp = p->vseq;
   					//cout << "list:" << pp << "  "<<v[pp].color<<endl;
   					if (v[pp].color == WHITE) {
   						tree.PushBack(pp, p->weight, p->eseq, tmp.seq);
   						v[pp].color = GRAY;
   						v[pp].d = t;
   						t++;
   						v[pp].parent = tmp.seq;
   						st.push(v[pp]);
   						p = p->next;
   						tmp.has = true;
   						break;
   					}
   					else if (v[pp].color == GRAY) {
   						p = p->next;
   					}
   					else if (v[pp].color == BLACK) {
   						p = p->next;
   					}
   				}
   				if (!tmp.has) {
   					//cout << tmp.seq << " has " << tmp.has << endl;
   					v[tmp.seq].color = BLACK;
   					v[tmp.seq].f = t;
   					t++;
   					st.pop();
   				}
   			}
   		}
   	}
   }

3. 得到不在树上的边

   void ninT() {//在T上，不在T上，eseq判断
   	for (int i = 0; i < E; i++) {
   		if (!tree.Finde(i)) {
   			ntree.push(e3[i]);
   		}
   	}
   }

4. 生成树的邻接链表

   一开始我直接用的整个生成图的邻接链表去DFS找环，后来想想不对，因为不是所有的边都在那个数+边里。

   //生成树的邻接链表
   void tlink() {
   	//intialize e2  or clear
   	if (countt > 1) {
   		for (int i = 0; i < V; i++) {
   			for (int j = 0; j < e2[i].count; j++) {
   				Node * kk = e2[i].head;
   				e2[i].MovNode(kk);
   				j--;
   				//kk = kk->next;
   			}
   		}
   	}
   	l = tree.head;
   	for (int i = 0; i < tree.count; i++) {
   		if (!e2[l->vseq].Find(l->vseq2)) {
   			e2[l->vseq].PushBack(l->vseq2, l->weight, l->eseq, l->vseq);
   			e2[l->vseq2].PushBack(l->vseq, l->weight, l->eseq, l->vseq2);
   		}
   		l = l->next;
   	}
   }

5. 找环

   原来是一棵树，加上一条边，一定有一个环，且新加的这条边一定在环上。设这条新加的边为(a,b)，则以a为起始点做DFS，遇到第一条返回边时，这个环就找到了。（无向图只有树边和返回边）

   在实现过程中，我先将新加的边加入到生成树中，再生成邻接链表，在DFS过程中，只记录返回边，环根据父节点可以得到。（从返回边的一端回溯，到另一端点，就能找出这个环）

   得到了环之后，就可以找出环上权重最大的边删除。一直循环到所有不在T上的边都试了一次。

   //找环
   void findc() {
   	//加边
   	while (!ntree.empty()) {
   		countt++;
   		//cout << countt << endl;
   		//Node *r = ntree.top();//一条不在t的边
   		Edge r = ntree.top();
   		//----------------------------
   		tree.PushBack(r.vseq,r.weight,r.eseq,r.vseq2);
   		tlink();
   		
   		//dfs找环退出
   		//要按tree中的边dfs，不能按原来的
   		t = 0;
   		for (int i = 0; i < V; i++) {
   			v2[i].seq = i;
   			v2[i].color = WHITE;
   			v2[i].d = -1;
   			v2[i].f = -1;
   			v2[i].parent = V;
   		}
   		//push the first
   		//新加的边必定在环内，以该边的一点为dfs的起始点，找到返回边，说明有环
   		//无向图只有树边和返回边
   		//for (int s = 0; s < V; s++) {
   		int s = r.vseq;
   		if (v2[s].color == WHITE) {
   			//cout << v[s].seq << endl;
   			v2[s].color = GRAY;
   			v2[s].d = t;
   			t++;
   			st2.push(v2[s]);
   			while (!st2.empty()) {
   				tmp = st2.top();
   				//cout << tmp.seq << " color:" << tmp.color << endl;
   				if (v2[tmp.seq].color == BLACK) {
   					st2.pop();
   				}
   				//cout << "top: " << tmp.seq << endl;
   				//adjacent
   				p = e2[tmp.seq].head;
   				for (int i = 0; i < e2[tmp.seq].count; i++) {
   					pp = p->vseq;
   					//cout << "list:" << pp << "  "<<v[pp].color<<endl;
   					if (v2[pp].color == WHITE) {
   						//tree.PushBack(pp, p->weight, p->eseq, tmp.seq);
   						v2[pp].color = GRAY;
   						v2[pp].d = t;
   						t++;
   						v2[pp].parent = tmp.seq;
   						st2.push(v2[pp]);
   						p = p->next;
   						tmp.has = true;
   						break;
   					}
   					else if (v2[pp].color == GRAY) {
   						if (pp != v2[p->vseq2].parent) {
   							cir.PushBack(pp, p->weight, p->eseq, p->vseq2);
   						}							
   						p = p->next;
   						//break;
   						//continue;
   					}
   					else if (v2[pp].color == BLACK) {
   						p = p->next;
   					}
   
   				}
   				if (!tmp.has) {
   					//cout << tmp.seq << " has " << tmp.has << endl;
   					v2[tmp.seq].color = BLACK;
   					v2[tmp.seq].f = t;
   					t++;
   					//tmp.color = BLACK;
   					//tmp.f = t;
   					//t++;
   					st2.pop();
   				}
   
   			}
   		}
   		//}
   		//---------------------------------------
            //环
   		Node *u = cir.head;
   		int k = L;
   		int h = L;
   		int w = L;
   		while (k != s) {
   			k = v2[u->vseq2].parent;
   			h = e[u->vseq2].finde(k, u->vseq2);
   			w = e3[h].weight;
   			//cout << u->vseq2 << " " << k << " " << endl;
   			cir.PushBack(u->vseq2,w,h,k);
   			u = u->next;
   		}
   		//-----------------
   		//环中最大的
   		u = cir.head;
   		//Node *m = u;
   		int maxw = -1;
   		int maxseq = u->eseq;
   		for (int i = 0; i < cir.count; i++) {
   			if (u->weight > maxw) {
   				maxseq = u->eseq;
   				maxw = u->weight;
   			}
   			u = u->next;
   		}
   		//---------------------
   		//删除最大的
   		u = tree.head;
   		for (int i = 0; i < tree.count; i++) {
   			if (u->eseq == maxseq) {
   				tree.MovNode(u);
   				break;
   			}
   			u = u->next;
   		}
   		ntree.pop();
   		//------------
   		//intializa tree			
   		for (int j = 0; j < cir.count; j++) {
   			Node * kk = cir.head;
   			cir.MovNode(kk);
   			j--;
   			//kk = kk->next;
   		}	
   	}	
   }

6. 我选择用kruskal算法进行验证

   重点是并查集find和unite的实现。

   int find(int x) {
   	int root = x;
   	while (root != par[root]) root = par[root];
   	while (x != root) {
   		int t = par[x];
   		par[x] = root;
   		x = t;
   	}
   	return root;
   }
   void unite(int x, int y) {
   	x = find(x);
   	y = find(y);
   	if (Rank[x] < Rank[y]) {
   		par[x] = y;
   	}
   	else {
   		par[y] = x;
   		if (Rank[x] == Rank[y]) Rank[x]++;
   	}
   }
   void mst_kruskal() {
   	for (int i = 0; i < E; i++) {
   		e4[i] = e3[i];
   		//cout << e4[i].vseq << "  " << e3[i].vseq << endl;
   	}
   	for (int i = 0; i < V; i++) {
   		//set[i].PushBack();
   		par[i] = i;
   		Rank[i] = 0;
   	}
   	Edge tempp;
   	for (int i = 0; i < E-1; i++) {
   		for (int j = i + 1; j < E; j++) {
   			if (e4[i].weight > e4[j].weight) {
   				tempp = e4[j];
   				e4[j] = e4[i];
   				e4[i] = tempp;
   			}
   		}
   	}
   	for (int i = 0; i < E; i++) {
   		int vv = e4[i].vseq;
   		int uu = e4[i].vseq2;
   		//cout << vv << " " << v[vv].set << " " << uu << " " << v[uu].set << endl;
   		if (find(vv) != find(uu)) {
   			A.PushBack(vv,e4[i].weight, e4[i].eseq, uu);
   			//v[uu].set = v[vv].set;
   			unite(vv, uu);
   		}
   	}
   }

7. main函数

   输出局部搜索算法和Kruskal算法的最小生成树的权重进行比较，如果相等，则证明正确。

   int main()
   {
   	creDGra();
   	for (int i = 0; i < V; i++) {
   		cout << i;
   		e[i].PrintList();
   	}
   	cout << "----------------------------" << endl;
   	DFS();
   	ninT();
   	findc();
   	cout << "=============================" << endl;
   	int sum1 = 0;
   	//tree.PrintList();//最小生成树
   	//----------------------
   	l = tree.head;
   	for (int i = 0; i < tree.count; i++) {
   		cout << l->vseq << " " << l->vseq2 << " " << l->weight << " " << l->eseq << endl;
   		sum1 += l->weight;
   		l = l->next;
   	}
   	cout << "局部搜索:";cout << sum1 << endl;
   	//-------------------------
   	cout << "----------------------------" << endl;
   	int sum2 = 0;
   	mst_kruskal();
   	l = A.head;
   	for (int i = 0; i < A.count; i++) {
   		sum2 += l->weight;
   		cout << l->vseq << " " << l->vseq2 << " " << l->weight << " " << l->eseq << endl;
   		l = l->next;
   	}
   	cout << "kruskal：" << sum2 << endl;
   	getchar();
       return 0;
   }

8. 结果截图

   

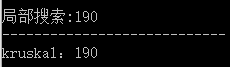
完成，✿✿ヽ(°▽°)ノ✿

赏

谢谢你请我吃糖果